Common Core Nuggets :: Pythagorean Theorem
This collection contains apps that will help teachers implement Common Core Standard 8.G.6 for 8th grade mathematics.
This collection contains apps that will help teachers implement Common Core Standard 8.G.6 for 8th grade mathematics.
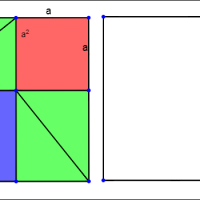
This app allows you to explore geometric proof offered by Greek mathematician Pythagoras himself.
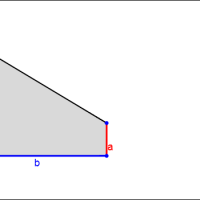
This app allows you to explore the algebraic proof offered by James A. Garfield, the twentieth president of the United States. He discovered this proof five years before he became the President.
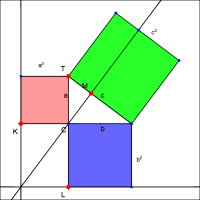
This app allows you to explore geometric proof that is a variation of the original Euclid's proof. In this proof, the shear transformation is used to change the shapes without changing their areas.
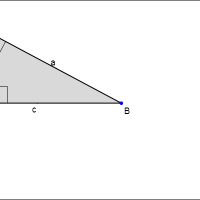
This app allows you to explore algebraic proof by the ancient Hindu mathematician Bhaskara, who used the properties of similarity to prove the theorem.